Synergizing Quantum Computing and AI: Correcting Quantum Errors in the Age of AI
2 years ago
Quantum computers have attracted significant attention in recent years due to their vast potential to revolutionise various scientific, industrial and computing fields. With their ability to exploit quantum mechanics phenomena such as superposition and entanglement, quantum computers promise to solve complex problems exponentially faster than standard computers.
This extraordinary computing power is essential for unlocking breakthroughs in areas such as cryptography, optimisation, drug discovery and the simulation of quantum systems. However, the influential power of quantum computers comes with a fundamental challenge, which is dealing with errors. Unlike classical computers, which rely on stable and reliable bits of information, quantum computers are extremely sensitive to errors caused by environmental noise, hardware imperfection, and quantum operations. These errors result from decoherence, a process in which quantum systems lose their fragile quantum states and become entangled with the surrounding world. Because Quantum Computing involves manipulating and measuring quantum states, errors can quickly propagate and amplify, leading to exponential degradation of results. The fragility of quantum information poses a significant obstacle to the make practical use of quantum computers.
Artificial intelligence algorithms have proven to be a powerful tool that, interestingly, can also be used to address the challenges that are an inherent part of Quantum Computing. This synergy between AI and Quantum Computing applies to various challenges, such as designing quantum simulations, enhancing quantum error-correction codes, searching for new medications and developing secure quantum-resistant encryption techniques that protect data against potential quantum threats. Overall, AI is a critical ally in introducing Quantum Computing by providing the tools and strategies necessary to harness the potential of quantum computers in a more practical and reliable manner. The collaborative potential of machine learning and Quantum Computing is instrumental in overcoming the fragility of quantum information and harnessing the substantial computational power that quantum systems offer. This partnership between machine learning and Quantum Computing promises significant breakthroughs across scientific, industrial, and computing domains, marking a real step towards realising the full potential of quantum computing.
In today's blog article, I would like to focus on a specific use-case where AI supports Quantum Computing, which is decoding topological quantum codes, particularly the frequently used Toric code [1]. However, we will not delve into the principles of topological codes or even of Quantum Computing, but only present on a high level the problem and the benefits of AI-based solutions
Quantum Error Correction Codes
The aim of quantum error correction codes is to redundantly encode logical qubits into a more extensive set of physical qubits to protect quantum information. In a similar way, we often proceed in classical algorithms to create in advance the fact of the emergence of an error in the course of information transfer/processing. These codes introduce redundancy in a clever way that allows for effective detection and correction of errors without direct access to delicate quantum states. By encoding logical information in a redundant and fault-tolerant manner, quantum error correction enables reliable Quantum Computing, even in the presence of errors. Among the distinct types of quantum codes, topological codes have gained considerable attention due to their unique properties and fault tolerance.
Topological codes were inspired by the concepts of topology, an essential branch of mathematics that unravels the properties and relationships of geometric objects, and offer an intriguing approach to quantum error correction. Topological codes exploit the fact that qubits have non-local, collective properties that protect against errors. In topological codes, a logical qubit is represented by a non-local property shared by a group of physical qubits rather than relying on the state of individual qubits. This non-local property is immune to local errors because the encoded information is distributed throughout the system. One topological coding implementation worth mentioning is the Toric code, which encodes quantum information in the form of non-trivial quantum states called logical operators, associated with loops or strings that wind around the torus. In 2021, the Google Quantum AI team was able to build a quantum processor based on topological ordered states [2], and the resulting effect confirms the potential in applying such a solution in quantum error correction.
Topological codes are among the most appealing candidates for the practical implementation of Quantum Computing because they can be instantiated on a two-dimensional lattice of qubits with local control operators. Those local control operators, so-called stabiliser operators, allow the detection of the error in the encoded state by conducting measurements on them. The outcome of those measurements is called a syndrome, which indicates the existence of an error.
The need to decode topological codes
Unfortunately, in Toric code, the syndromes are not unique. Due to degeneration, varying error combinations can yield the same syndrome. An error in Toric code commonly generates a non-trivial syndrome by inverting some stabiliser operators. However, many different varieties of errors can lead to the same reversed operators and therefore produce the same syndrome, as shown in Figure 2 below. This syndrome degeneration can complicate the error correction process because it imposes vagueness in identifying the specific error that caused the monitored syndrome. Choosing the most appropriate correction chain is called decoding, and it is a non-trivial task. The algorithms that accomplish this task are called decoders.
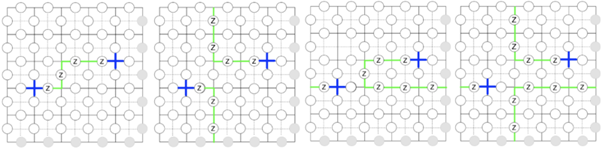
Figure 2. Four strings of Z errors with the same syndrome. You do not need to understand the origin of these visualisations. However, note that different error paths (green routes) lead to the same syndrome (blue crosses).
In quantum codes, decoding is crucial as it involves identifying and locating errors that occur during quantum computation. This information is then used to apply corrective measures and restore the original quantum-state. However, decoding quantum codes in real-time scenarios is challenging for several reasons. Real-time decoding involves a trade-off between speed and accuracy, as fast decoding may lead to errors, while accurate decoding may not meet real-time requirements. The limited processing time and resources in fast decoding may cause errors or sub-optimal corrections. Conversely, striving for greater accuracy may result in slower decoding, potentially failing to meet real-time requirements. Decoding requires measurements over many physical qubits, which can be time-consuming. In real-time applications, decoding must be performed quickly enough to keep up with ongoing quantum computations. Despite theoretical advances in quantum error correction, the practical implementation and scalability of decoding codes in quantum computers still need to be improved.
AI and Quantum Codes Decoding
Recent research has indicated that machine learning techniques can overcome the challenges of decoding quantum codes [3, 4, 5, 6]. In particular, deep learning algorithms that rely on artificial neural network models have demonstrated their ability to learn complex mappings and make predictions from enormous amounts of data. By training neural networks on synthetic or simulated data, their capacity can be utilised to comprehend complex error patterns and infer underlying error configurations. Using neural decoders to decode quantum codes has many advantages. Firstly, neural decoders can identify compound relationships between ensembles and error configurations, which could potentially outperform traditional decoding algorithms. Neural network models can also generalise enough to take into account unseen syndromes, which results in more dependable decoding performance. Deep learning-based decoders can also be trained to adapt to different noise models, making them versatile and applicable to other quantum hardware platforms.
It is essential to distinguish between two approaches of decoding strategy: low-level and high-level decoding [7]. Low-level decoding refers to decoding strategies that operate at the level of the code's physical qubits (ancilla qubits). Low-level decoders receive the error syndrome and promptly produce an error probability distribution for every ancilla qubit by taking into account the observed syndrome. This process is designed to rectify all physical errors that may have taken place. On the other hand, high-level decoding strategies aim to decode the code more abstractly, leveraging the logical operators and prediction of logical qubits (data qubits) errors rather than physical qubits. High-level decoders confidently generate an error probability for the logical state of the data qubit based on the error syndrome input. This eliminates the need to predict corrections for all data qubits because the decoder only needs to focus on the state of the logical qubit. Therefore, the prediction process is simplified, making decoding more efficient.
Covering both low-level and high-level decoding, AI-based techniques could help revitalise quantum error correction, offering the promise of more efficient and flexible decoding strategies that improve the reliability and performance of quantum hardware platforms. As artificial intelligence continues to advance in this field, it has the potential to unlock the full power of Quantum Computing by driving innovations that could transform our understanding of the quantum realm and redefine the limits of computational capabilities.
Conclusions
Today's blog article gives an optimistic picture of quantum computing development. It should be noted that, although the realm of quantum computing is advancing rapidly, developing genuinely useful computers is still a long way off, probably many years from now. Nevertheless, it should be recognised that one of the tools that can accelerate the development of the field of quantum computing is AI, especially deep learning methods. Neural decoders harness the power of deep learning algorithms to automatically learn and optimise the decoding process, potentially leading to more efficient and accurate error correction.
[1] Kitaev, A. Yu. “Fault-tolerant quantum computation by anyons.” Annals of Physics 303.1 (2003): 2-30.. (arXiv)
[2] Satzinger, K. J., et al. “Realizing topologically ordered states on a quantum processor.” Science 374.6572 (2021): 1237-1241.. (arXiv)
[3] Torlai, G., & Melko, R. G. “Neural Decoder for Topological Codes” (arXiv)
[4] Bordoni, S., & Giagu, S. “Convolutional neural network based decoders for surface codes” (link)
[5] Choukroun, Y., & Wolf, L. “Deep Quantum Error Correction” (arXiv)
[6] Krastanov, S., & Jiang, L. “Deep Neural Network Probabilistic Decoder for Stabilizer Codes” (arXiv)
[7] Varsamopoulos, S., Bertels, K., & Almudever, C. G. “Comparing Neural Network Based Decoders for the Surface Code”, IEEE Transactions on Computers, 300-311.. (arXiv)